본 문서는 회전자 분석 기법 SPM, Stator-pole mapping에 대해 설명을 합니다.

---

모터 성능은 역기전력을 측정하여 평가할 수 있습니다. 역기전력이란 외부에서 모터 축을 회전시킬 때 고정자 코일에 유도되는 전압을 의미합니다. 패러데이 전자기 유도 법칙에 따라, 축이 회전하면 코일에 인가되는 자기장 B가 변하면서 전압이 유도되는거죠. 만약 모터 축을 일정한 속도로 회전시킨다면, 역기전력은 정현파 (sine wave) 형태로 출력이 되며, 파형의 크기 (진폭) 및 왜곡 (THD)을 측정하여 양품과 불량을 판정할 수 있습니다. 만약 자석의 세기가 줄어들면 비례하여 진폭이 줄어들고, 또는 N-S-S-N-S … 순서로 잘못 조립되면 파형의 왜곡이 커지겠죠.

회전자의 자기 특성 측정 방법은 역기전력 특성과 상관관계가 있어야 합니다. 이를 위해 역기전력이 어떻게 생성되는지 다시한번 짚어봅시다. 모터 한 상의 코일에 유도되는 전압은 어떻게 계산할 수 있을까요? 패러데이 전자기 유도 법칙에 따르면 유도기전력 e는 자속의 변화량에 비례합니다.

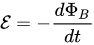
우선 자속에 대해 알아봅시다. 자속량을 계산하려면 공업수학 시간에 배운 면적분 (…) 공식이 필요한데, 그건 너무 복잡하니 단순하게 면적 A=1㎡, 권선수 N=1인 코일에 자기장 B가 균일하게 수직방향으로 B=1T가 인가된다고 가정해봅시다. 이때 자속은 1㎡*1*1T=1Wb가 됩니다. 자속량 웨버, Wb는 이렇게 정의됩니다.

만약 이 코일에 1초동안 자기장이 0->1T로 변하면 자속 역시 0->1Wb로 변하고, 유도기전력은 상기 수식에 따라 1V가 출력됩니다. 이 때문에, 자속의 측정 단위로 Wb 대신 V*s를 사용하기도 합니다. 다음은 자속이 정현파 형태, Φ(t)=sin(t)라고 가정을 해봅시다. sin 미분은 sin이기 때문에, 유도기전력 e(t)=-sin(t)가 됩니다. 이번에는 코일의 권선수를 10으로 증가시켜봅시다. 이때 유도되는 역기전력은 e(t)=10*sin(t)[V]가 됩니다.

다시 모터 회전자 측정 문제로 돌아옵시다. 역기전력을 측정하려면 회전자 자속을 측정해야 하는데, 어떻게 측정해야 할까요? 가장 간단한 방법은 코일을 고정자 크기와 비슷한 형태로 권선하고, 회전자를 회전시키는 방법입니다. 이 방법이 가장 좋기는 한데, 현실적인 문제가 몇가지 있습니다.

가장 큰 문제는 신호대 잡음 비 입니다. 코일에 유도되는 역기전력을 증가시키려면 측정 RPM을 증가시켜야 하는데, 이 경우 회전시키는 모터의 노이즈 역시 증가합니다. 또한 이렇게 고속으로 회전시키려면 측정 기구가 매우 견고해야 하는데, 일반적으로 주철 정반을 가공해서 제작해야 합니다.

현장에서 대안으로 사용하는 방법은 자속을 측정하는 대신, 홀 센서를 이용하여 표면의 자속밀도 B를 측정하는 방법입니다. 모터를 이용하여 회전자를 낮은 RPM으로 회전시키고 (30~40RPM), 홀 센서 배열을 이용하여 고정자 코일 위치에서 자기장을 측정하면 표면 자속밀도 (heatmap) 데이터를 얻을 수 있습니다.

홀 센서는 자기장에 비례하여 전압을 출력하기 때문에 측정 대상을 빨리 회전시킬 필요가 없어 안정적으로 데이터를 측정할 수 있고 더불어 측정 기구가 간단해집니다. 다만 문제점은 우리가 측정한 데이터가 자기장 B이지, 자속 Φ가 아니라는 점 입니다. 역기전력은 자속의 변화량이기 때문에 자기장 데이터를 자속량으로 변화시켜야 하고, 이때 사용되는 알고리즘이 stator-pole mapping 입니다.

Stator-pole mapping 알고리즘은 매우 간단합니다. 회전자가 회전할 때 고정자 한 폴에 들어가는 자기장 데이터 B를 모두 더한 값 입니다. 만약 고정자가 30도 각도를 가진다고 가정해봅시다. 회전자가 0도 위치에 있을 때, 고정자에 들어가는 값은 -15도에서 +15도까지 자기장 값을 모두 더하면 되겠죠? 회전자가 1도 위치면 [-14,16]도 범위의 값을 더하고, x도 위치에 있다면 [x-15,x+15] 영역의 값을 모두 더하면 되겠죠. 사실 이건 신호처리의 moving average filter와 동일한 알고리즘입니다.

Note

엄밀하게 이야기 하면, 자기장 B*센서의 측정영역 ds를 곱해줘야 자속 Φ가 됩니다.

다음은 두 종류 회전자의 표면 자속 밀도 B를 측정한 데이터 입니다. 그림에서 바로 알 수 있듯이, 한 회전자는 skew가 있고 다른 회전자는 skew가 없는 회전자입니다.

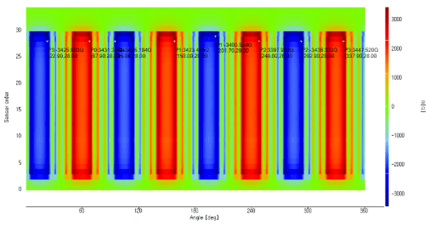
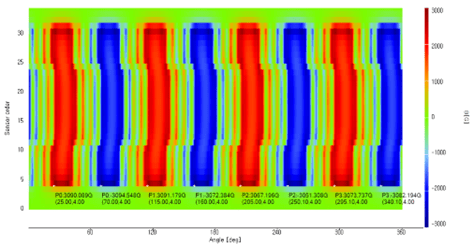
이 두 자속밀도 B 데이터를 SPM을 이용하여 자속으로 변환하면 어떻게 될까요? 파란색은 skew가 없는 회전자, 주황색은 skew가 있는 회전자의 SPM 변환 결과 입니다. 두 파형의 차이가 보이시나요? Skew가 없는 회전자는 진폭이 크지만 왜곡 또한 큽니다. 반대로, skew가 있는 회전자는 진폭은 줄지만 왜곡이 훨씬 적음을 확인할 수 있습니다. 아래 결과는 SPM 변환이 역기전력 특성을 반영하고 있다는 것을 보여줍니다.